浮点数设计原理

参考

《Go语言底层原理剖析》第2章浮点数设计原理与使用方法

浮点数的二进制表示 - 阮一峰的网络日志

1 从一个例子说起

package main

import "fmt"

func main() {
  var d1, d2 float64
  d1 = 0.3
  d2 = 0.6
  fmt.Println(d1 + d2) // 0.8999999999999999

  var f1 f2 float32
  f1 = 0.3
  f2 = 0.6
  fmt.Println(f1 + f2) // 0.90000004
}

上面的浮点数计算的结果与我们想象的好像不太一样，为什么0.3+0.6的结果不是0.9呢？

下面将展开讲解浮点数在计算机中的 存储方式 以及精度损失的概念，最后对这个🌰进行解释。

2 存储方式

众所周知，所有数据在计算机中都是以二进制的形式进行存储的。整数比较简单，转换为二进制数即可，而小数怎么转换呢？尤其是3.141592…这种无限小数如何利用有限的二进制位进行存储呢？

小数目前有两种存储方式：定点数 & 浮点数。计算机中采用的是浮点数。

2.1 定点数

定点数比较简单，固定小数点的位置，小数点前的二进制数表示整数部分 & 小数点后的二进制数表示小数部分。

但是对于0.1234…这种整数部分很小或者…12345.1这种整数小数部分精度很低的数据，定点数就不适合了，它的扩展性很差。

2.2 浮点数

浮点数小数点的位置是浮动的(不固定)，采用科学计数法来表示：
$$
V = (-1)^S \times M \times R^E
$$
S表示符号位、M表示尾数、R表示基数、E表示指数

例如十进制3.1415小数用科学计数法可以表示为：
$$
3.1415 = 3.1415 * 10^0
$$
$$
3.1415 = 31.415 * 10^{-1}
$$
$$
3.1415 = 314.15 * 10^{-2}
$$
那么采用哪种方式来表示？指数位和尾数位各应该是多少？这就得引入 IEEE754 浮点数标准

2.3 IEEE754浮点数标准

该标准规定科学计数法底数R=2：
$$
V = (-1)^S \times M \times 2^E
$$
还规定对于32位浮点数。最高1位是符号位S，中间8位是指数E，最后23位是尾数M

对于64位浮点数。最高1位是符号位S，中间11位是指数E，最后52位是尾数M

需要注意的是，转化为二进制后M是一个01串，可以将其向左平移至整数位为1，此时M的第一位始终为1，为了节省空间从而增大精度可以直接把1去掉。

举个🌰：0.75的二进制为0.11000…，向左平移后：1.100…，再把整数位的1去掉：0.100…，于是0.75的尾数为1000…

package main

import (
  "fmt"
  "math"
)

func main() {
  calfloat(0.75)
}

func calfloat(x float32) {
  f := math.Float32bits(x)
  bits := fmt.Sprintf("%.32b", f)
  fmt.Println("float32:", x)
  fmt.Println("bits:", bits)
  fmt.Println("S:", bits[0:1])
  fmt.Println("E:", bits[1:9])
  fmt.Println("M:", bits[9:])

  bias := 127 // 偏移量
  sign := f & (1 << 31)
  exponentRaw := int(f >> 23)
  exponent := exponentRaw - bias
  var mantissa float32
  for index, bit := range bits[9:] {
    if bit == '1' {
      bitValue := math.Pow(2, float64(index+1))
      mantissa += float32(1 / bitValue)
    }
  }

  value := (1 + mantissa) * float32(math.Pow(2, float64(exponent)))
  fmt.Printf("sign: %d,  Exponent: %d(%d)  Mantissa: %f  Value: %f \n", sign, exponentRaw, exponent, mantissa, value)
}

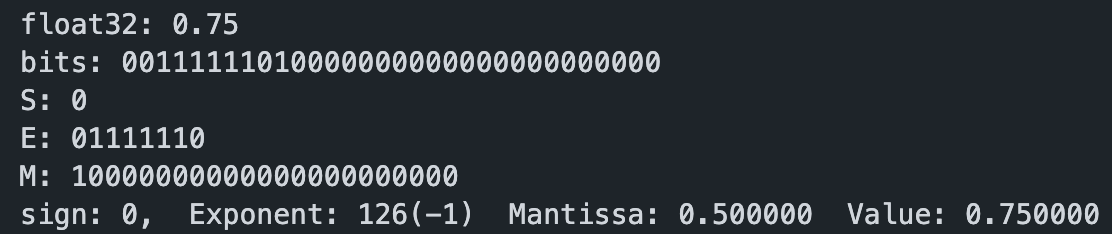
其中bias表示偏移量，这是为了表达负数，对于32位浮点数，把[0, 2^8-1]即[0, 255]偏移到[-127, 128]需要减去127。对于64位浮点数bias=1023

3 浮点数精度

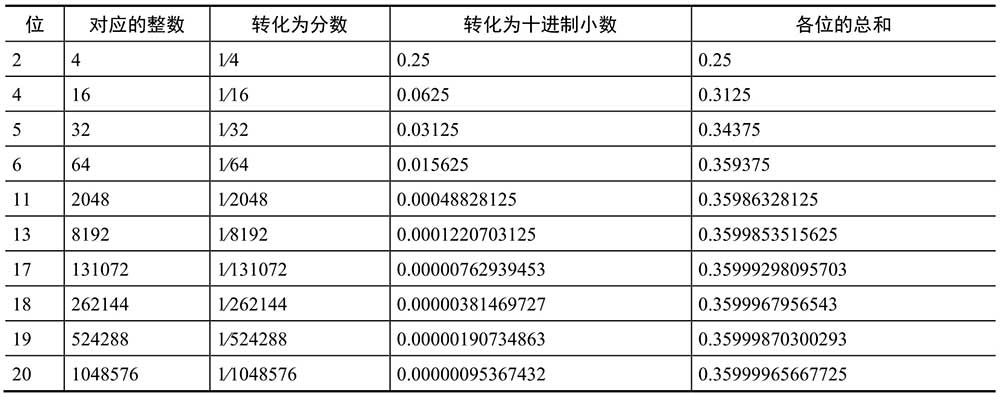
一般讨论浮点数精度针对的是十进制下的浮点数，实际上浮点数的精度是不固定的，单精度浮点数float32的精度为6～8位，双精度浮点数float64的精度为15～17位。

浮点数的定义：在一个范围内，将d位十进制数（按照科学计数法表达）转换为二进制数，再将二进制数转换为d位十进制数，如果数据转换不发生损失，则意味着在此范围内有d位精度。

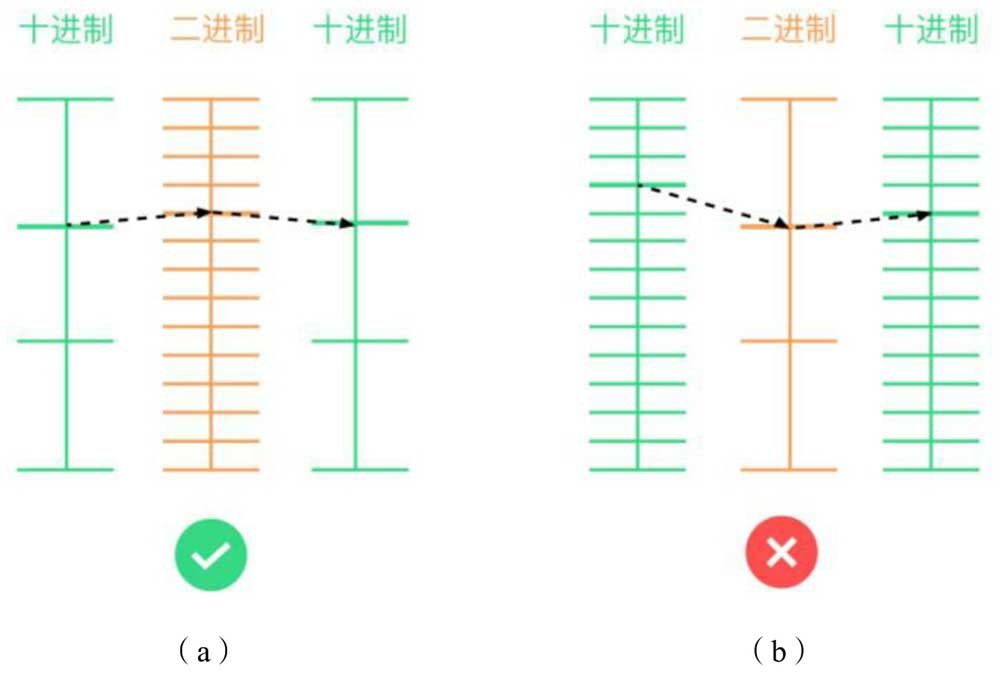
精度存在的原因在于，数据在进制之间相互转换时，不是精准匹配的，而是匹配到一个最接近的值。

如图(a)所示，十进制数转换为二进制数，二进制数又转换为十进制数，如果能够还原为最初的值，那么转换精度是无损的，说明在当前范围内浮点数是有d位精度的。反之，如图(b)所示，d位十进制数转换为二进制数，二进制数又转换为d位十进制数，得到的并不是原来的值，那么说明在该范围内浮点数没有d位精度。

4 回到最初的例子

为什么单精度浮点数&多精度浮点数表达0.3+0.6会有不同的结果呢？

首先需要明确的是fmt.Println fmt.Printf 内部对浮点数进行了复杂的运算，将其转换为了最接近的十进制数。

  x := float32(0.90000000)
  fmt.Printf("%f\n", x) // 0.900000
  fmt.Printf("%.7f\n", x) // 0.9000000
  fmt.Printf("%.8f\n", x) // 0.89999998
  fmt.Printf("%.9f\n", x) // 0.899999976

默认打印小数点后6位，单精度浮点数在存储和表示0.9时精度为7，小数点后八位开始就有精度问题了。

实际上，除了浮点数表示会丢失精度，浮点数计算也会丢失精度，那么例子里是什么原因导致精度丢失到呢？下面再做个实验

  var d1, d2 float64
  d1 = 0.4
  d2 = 0.5
  fmt.Println(d1 + d2) // 0.9

  var f1, f2 float32
  f1 = 0.4
  f2 = 0.5
  fmt.Println(f1 + f2) // 0.9

0.4+0.5并没有丢失精度，那么可以基本判断例子中是因为浮点数计算导致的精度丢失。

对于单精度浮点数

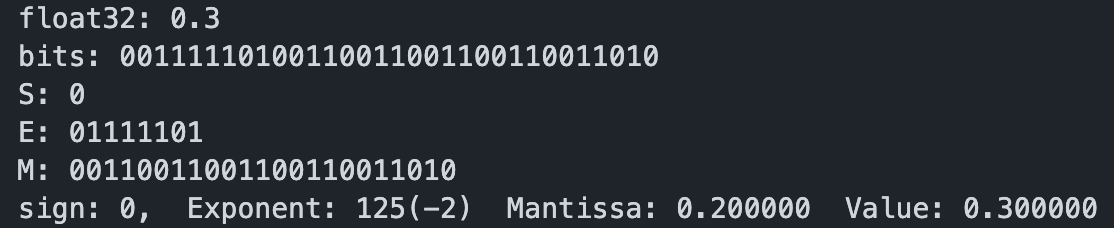
0.3的二进制：(1.00110011001100110011010x2^-2) -> 0.0100110011001100110011010 -> (0.30000001192092896)实际上不等于0.3
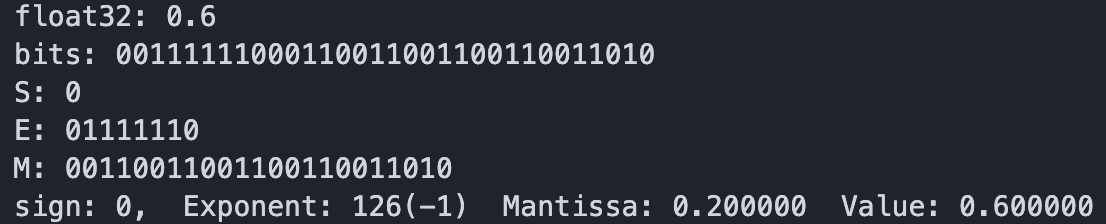
0.6的二进制：(1.00110011001100110011010x2^-1) -> 0.10110011001100110011010 -> (0.7000000476837158) 实际上不等于0.6
0.3+0.6= ：0.1110011001100110011001110
转为十进制为 0.90000004

对于双精度浮点数

func calfloat(x float64) {
  f := math.Float64bits(x)
  bits := fmt.Sprintf("%.64b", f)
  fmt.Println("float64:", x)
  fmt.Println("bits:", bits)
  fmt.Println("S:", bits[0:1])
  fmt.Println("E:", bits[1:12])
  fmt.Println("M:", bits[12:])

  bias := 1023
  sign := f & (1 << 63)
  exponentRaw := int(f >> 52)
  exponent := exponentRaw - bias
  var mantissa float64
  for index, bit := range bits[12:] {
    if bit == '1' {
      mantissa += math.Pow(2, -1*float64(index+1))
    }
  }

  value := (1 + mantissa) * float64(math.Pow(2, float64(exponent)))
  fmt.Printf("sign: %d,  Exponent: %d(%d)  Mantissa: %f  Value: %f \n", sign, exponentRaw, exponent, mantissa, value)
}

0.3的二进制：0.010011001100110011001100110011001100110011001100110011 实际上!=0.3
0.6的二进制：0.10011001100110011001100110011001100110011001100110011 实际上!=0.6
0.3+0.6= ：0.111001100110011001100110011001100110011001100110011001
转为十进制为 0.8999999999999999

由上可知，因为0.3和0.6都不能无损存储为二进制数，最后的计算结果也有精度的损失。

5 大数运算库

当float64的精度无法满足需求时，可以考虑使用math/big库,著名区块链项目以太坊即用该库来实现货币的存储和计算。虽然实测0.3+0.6还是有精度损失。

  d1, d2 := big.NewFloat(0.3), big.NewFloat(0.6)
  fmt.Println(d1.Add(d1, d2)) // 0.8999999999999999

但是该库对于大整数运算还是很好用的

  a, b := big.NewInt(0), big.NewInt(1)
  limit := a.Exp(big.NewInt(10), big.NewInt(99), nil)
  for a.Cmp(limit) < 0 {
    a.Add(a, b)
    a, b = b, a
  }
  fmt.Println(a)
  // 1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000